BondOrderParameters class¶
This class defines a set of parameters for a bond order factor, to be used in conjunction with the Coordinator class.
Similarly to the potentials, the available types of bond order factors are always inquired from the Fortran core to ensure that any changes made to the core are automatically reflected in the Python interface.
The same utility functions in pysic for inquiring keywords and other data needed for creating the potentials also work for fetching information on bond order factors, if applicable. The functions check automatically if the inquired name matches a potential or a bond order factor and gather the correct type of information based on this.
For example:
- Inquire the names of available bond order factors: list_valid_bond_order_factors()
- Inquire the names of parameters for a bond order factors: names_of_parameters()
Bond order cutoffs¶
Atomic coordination is an example of a simple bond order factor. It is calculated by checking all atom pairs and counting which ones are “close” to each others. Close naturally means closer than some predefined cutoff distance. However, in order to make the coordination a continuous and differentiable function, a continuous cutoff has to be applied. This is done similarly to the smooth cutoffs used in Potential by defining a proximity function which is 1 for small separations and 0 for large distances.
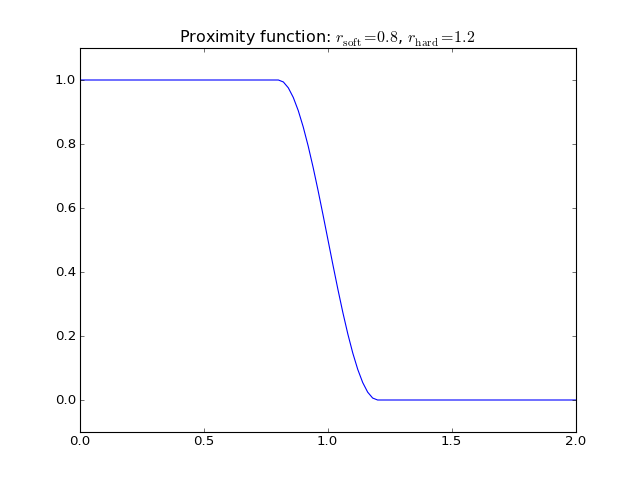
Since bond order factors such as atomic coordination need not decay as a function of distance, one must always define a margin for continuous cutoff in bond order factors.
Atomic and pairwise factors¶
Two types of factors can be defined: atomic or pairwise (per bond) factors. Let us first give formal definitions for these types and then discuss the differences in their use and behavior.
Atomic factors¶
Atomic factors are of the form
where the local factors \(c_{ij\ldots}\) may have 2, 3, or more indices depending on how many bodies affect the factor. When this kind of a factor is applied on an \(n\)-body potential, \(v_{ij\ldots}\), an \(n\)-body factor is created as the average of the atomic factors
The resulting potential is then
where the summation goes over all \(n\)-chains.
Pairwise factors¶
Pairwise factors, on the other hand are only defined for pair potentials \(v_{ij}\). These factors scale the interaction by
where the summation goes over all pairs \((i,j)\). Note that this form requires \(b_{ij}\) to be symmetric with respect to \(i\) and \(j\). It would also be possible to define the factor through
where the sum goes over all indices — and thus over all pairs twice. Using the notation above, this is equivalent to
Clearly, \(b_{ij} = \frac{1}{2}(\tilde{b}_{ij}+\tilde{b}_{ji})\). The factor \(\tilde{b}_{ij}\) defined in this manner need not be symmetric, since the summation automatically leads to the symmetric form. Because of this, to avoid the need to force symmetry on \(b_{ij}\), Pysic calculates the pairwise factors using \(b_{ij} = \frac{1}{2}(\tilde{b}_{ij}+\tilde{b}_{ji})\). Therefore it is only necessary to implement the non-symmetric factors \(\tilde{b}_{ij}\).
It is important to note that any scaling functions are applied on the factors \(\tilde{b}_{ij}\), not on \(b_{ij}\). The difference can be seen with a simple example. Let our factor be \(\tilde{b}_{ij} = \sqrt{\sum_{k} c_{ijk}}\). Then, \(b_{ij} = \frac{1}{2} (\sqrt{\sum_{k} c_{ijk}} + \sqrt{\sum_{k} c_{jik}}) \ne \sqrt{\frac{1}{2}(\sum_{k} c_{ijk} + c_{jik})}\). Also note that Bond order mixing is not possible between atomic and pairwise factors.
Only use a pairwise factor with a pair potential! If a pairwise factor is applied on an \(n\)-body potential where \(n \ne 2\), it will automatically be zero. However, applying such a factor will result in the potential being multiplied by the factor, and so the potential becomes zero also.
Pairwise and atomic factors can be used on one and the same pair potential, in which case they are simply added together:
The usefulness of this is probably limited — this behavior is adopted to avoid conflicts.
Defining parameters¶
A BondOrderParameters instance defines the type of the bond order factor, the cutoffs, and parameters for one set of elements. The parameters are formally split to scaling function parameters and local summation parameters, where for a factor of type
\(s_i\) is the scaling function and \(\sum_j c_{ij}\) is the local sum (similarly for many-body factors).
This division is mostly cosmetic, though, and the parameters could just as well be defined as a single list.
Bond order factors are applied and parameterized by atomic element types (chemical symbols). An \(n\)-body factor must always have one or several sets of \(n\) symbols to designate the atoms it affects. So, 2- and 3-body factors could accept for instance the following lists of symbols, respectively:
>>> two_body_targets = [['H', 'H'], ['H', 'O'], ['O', 'O']]
>>> three_body_targets = [['Si', 'O', 'H']]
Atomic factors¶
As an example, the Power decay bond order factor
is a two-body factor and therefore requires two elements as its target. It includes no scaling and two local summation factors.
Such a bond order factor could be created with the following command:
>>> bonds = pysic.BondOrderParameters('power_bond', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['Si', 'Si']],
... parameters=[[],[a, n]])
or alternatively in pieces by a series of commands:
>>> bonds = pysic.BondOrderParameters('power_bond')
>>> bonds.set_cutoff(3.2)
>>> bonds.set_cutoff_margin(0.4)
>>> bonds.set_symbols([['Si', 'Si']])
>>> bonds.set_parameter_value('a', a)
>>> bonds.set_parameter_value('n', n)
To be used in calculations, this is then passed on to a Coordinator, Potential, and Pysic with:
>>> crd = pysic.Coordinator( bonds )
>>> pot = pysic.Potential( ... , coordinator=crd )
>>> cal = pysic.Pysic( potentials=pot )
The above factor will only consider Si-Si pairs in the local summation \(b_i = \sum_j c_{ij}\), i.e., the atoms \(i\) and \(j\) must both be silicons. If also, say Si-O pairs should be taken into account, the list needs to be expanded:
>>> bonds.add_symbols([['Si','O']])
>>> bonds.get_symbols()
[['Si', 'Si'], ['Si', 'O']]
This will apply the factor on Si atoms so that the summation \(b_i = \sum_j c_{ij}\) goes over Si-Si and Si-O pairs, i.e., atom \(i\) is Si but atom \(j\) may be either Si or O.
If you want to define a bond factor also for oxygens, this can be done separately with for instance:
>>> bonds2 = pysic.BondOrderParameters('power_bond', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['O', 'O'], ['O', 'Si']],
... parameters=[[],[a, n]])
>>> crd2 = pysic.Coordinator( bonds2 )
>>> pot2 = pysic.Potential( ... , coordinator=crd2 )
>>> cal.add_potential( pot2 )
Here one needs to be careful. If you apply a bond order factor on a potential, say a Si-O pair potential, the factor is applied on both Si and O atoms. However, if no parameters are applied for O, the factor for it is zero. That is, in the case of a Si-O pair (Si is \(i\) and O is \(j\)) the bond factor \(b_{ij} = \frac{1}{2}(b_i + b_j)=\frac{1}{2}b_i\), which may be not the intended result.
If you want to have different local parameters for the different pairs O-O and O-Si, you must define two BondOrderParameters objects and wrap them in a Coordinator:
>>> bonds_oo = pysic.BondOrderParameters('power_bond', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['O', 'O']],
... parameters=[[],[a_oo, n_oo]])
>>> bonds_osi = pysic.BondOrderParameters('power_bond', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['O', 'Si']],
... parameters=[[],[a_osi, n_osi]])
>>> crd3 = pysic.Coordinator( [bonds_oo, bonds_osi] )
>>> pot3 = pysic.Potential( ... , coordinator=crd3 )
>>> cal.set_potentials( [pot, pot3] )
That is, local summation is done using all the given parameters summed together. If you apply a scaling factor on a bond order factor, however, it is applied only once. The scaling is determined by the first BondOrderParameters object in the Coordinator which defines a scaling function and whose first target is the atom for which the factor is being calculated. This can be used for Bond order mixing.
As a rule of thumb, remember that one Potential can contain only one Coordinator, but a Coordinator can contain many BondOrderParameters. So if your bond order factor requires several sets of parameters due to the different element pairs, it is safest to define each set of parameters using its own BondOrderParameters object and wrap the parameters involved in one local summation in a Coordinator.
Pairwise factors¶
As an example, the Tersoff bond order factor
is a three-body factor (it includes terms depending on atom triplets \((i, j, k)\)) and therefore requires a set of three elements as its target. It incorporates two scaling and five local sum parameters. Such a bond order factor could be created with the following command:
>>> bonds = pysic.BondOrderParameters('tersoff', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['Si', 'Si', 'Si']],
... parameters=[[beta, eta],
... [a, c, d, h, mu]])
or alternatively in pieces by a series of commands:
>>> bonds = pysic.BondOrderParameters('tersoff')
>>> bonds.set_cutoff(3.2)
>>> bonds.set_cutoff_margin(0.4)
>>> bonds.set_symbols([['Si', 'Si', 'Si']])
>>> bonds.set_parameter_value('beta', beta)
>>> bonds.set_parameter_value('eta', eta)
>>> bonds.set_parameter_value('a', a)
>>> bonds.set_parameter_value('c', c)
>>> bonds.set_parameter_value('d', d)
>>> bonds.set_parameter_value('h', h)
>>> bonds.set_parameter_value('mu', mu)
The above example creates a bond order factor which is applied to all Si triplets (symbols=[[‘Si’,’Si’,’Si’]]). The command also assigns scaling parameters \(\beta\), \(\eta\), and \(\mu\), and local summation parameters \(a\), \(c\), \(d\), and \(h\). If there are other elements in the system besides silicon, they will be completely ignored: The bond order factors are calculated as if the other elements do not exist. If one wishes to include, say, Si-O bonds in the bond order factor calculation, the list of symbols needs to be expanded by:
>>> bonds.add_symbols([['Si', 'Si', 'O'],
... ['Si', 'O', 'Si'],
... ['O', 'Si', 'Si'],
... ['Si', 'O', 'O'],
... ['O', 'Si', 'O']])
>>> bonds.get_symbols()
[['Si', 'Si', 'Si'], ['Si', 'Si', 'O'], ['Si', 'O', 'Si'], ['O', 'Si', 'Si'], ['Si', 'O', 'O'], ['O', 'Si', 'O']]
The format of the symbol list is as follows. In each triplet, the first two symbols determine the bond on which the factor is calculated (atoms \(i\) and \(j\)). (For atomic factors, the first symbol determines the element on which the factor is applied.) The third symbol defines the other atoms in the triplets which are taken in to account (atom \(k\)). That is, in the example above, Si-(Si-O) bond parameters are included with:
>>> ['Si', 'O', 'Si']
O-(Si-O) with:
>>> ['Si', 'O', 'O']
Si-(O-Si) with:
>>> ['O', 'Si', 'Si']
and O-(O-Si) with:
>>> ['O', 'Si', 'O']
The definition is complicated like this to enable the tuning of parameters of all the various bond combinations separately.
Instead of giving a list of symbols to a single BondOrderParameters, one can define many instances with different symbols and different parameters, and feed a list of these to a Coordinator object.:
>>> bond_sioo = pysic.BondOrderParameters('tersoff', cutoff=3.2, cutoff_margin=0.4,
... symbols=[['Si', 'O', 'O']],
... parameters=[[beta_si, eta_si],
... [a_sio, c_sio, d_sio, h_sio, mu_si]])
>>> bond_sisio = pysic.BondOrderParameters('tersoff', cutoff=3.5, cutoff_margin=0.5,
... symbols=[['Si', 'Si', 'O']],
... parameters=[[beta_si, eta_si],
... [a_sisi, c_sisi, d_sisi, h_sisi, mu_si]])
>>> bond_list = [bond_sioo,bond_sisio]
>>> crd = pysic.Coordinator( bond_list )
The above example would assign the parameter values
This gives the user the possibility to precisely control the parameters, including cutoffs, for different elements.
Note that the beta, eta, and mu parameters are the same for both BondOrderParameters objects defined in the above example. They could be different in principle, but when the factors are calculated, the scaling parameters are taken from the first object in the list of bonds (bond_list) for which the first element is of the correct type. Because of this, the scaling parameters in bond_sisio are in fact ignored. This feature can be exploited for Bond order mixing.
For three different elements, say C, O, and H, the possible triplets are:
>>> [ ['H', 'H', 'H'], # H-H bond in an H-H-H triplet
... ['H', 'H', 'C'], # H-H bond in an H-H-C triplet
... ['H', 'H', 'O'], # H-H bond in an H-H-O triplet
... ['H', 'O', 'H'], # H-O bond in an H-H-O triplet
... ['H', 'O', 'C'], # H-O bond in an O-H-C triplet
... ['H', 'O', 'O'], # H-O bond in an O-H-O triplet
... ['H', 'C', 'H'], # etc.
... ['H', 'C', 'C'],
... ['H', 'C', 'O'],
... ['O', 'H', 'H'],
... ['O', 'H', 'C'],
... ['O', 'H', 'O'],
... ['O', 'O', 'H'],
... ['O', 'O', 'C'],
... ['O', 'O', 'O'],
... ['O', 'C', 'H'],
... ['O', 'C', 'C'],
... ['O', 'C', 'O'],
... ['C', 'H', 'H'],
... ['C', 'H', 'C'],
... ['C', 'H', 'O'],
... ['C', 'O', 'H'],
... ['C', 'O', 'C'],
... ['C', 'O', 'O'],
... ['C', 'C', 'H'],
... ['C', 'C', 'C'],
... ['C', 'C', 'O'] ]
In principle, one can attach a different set of parameters to each of these. Often though the parameters are mostly the same, and writing these kinds of lists for all possible combinations is cumbersome. To help in generating the tables, the utility method expand_symbols_table() can be used. For instance, the full list of triplets above can be created with:
>>> pysic.utility.convenience.expand_symbols_table([['C', 'O', 'H'],
... ['C', 'O', 'H'],
... ['C', 'O', 'H']])
List of currently available bond order factors¶
Below is a list of bond order factors currently implemented.
- Coordination scaling function
- Square root scaling function
- Tabulated scaling function
- Coordination bond order factor
- Power decay bond order factor
- Tabulated bond order factor
- Tersoff bond order factor
Coordination scaling function¶
1-body bond order factor defined as
where \(\Sigma_i\) is the bond order sum.
In other words, this factor only overrides the scaling function of another bond order factor when mixed. Especially, it is zero if not paired with other bond order factors.
Keywords:
>>> names_of_parameters('c_scale')
[['epsilon', 'N', 'C', 'gamma', 'min'], []]
Square root scaling function¶
1-body bond order factor defined as
where \(\Sigma_i\) is the bond order sum and \(\varepsilon\) is a scaling constant.
Keywords:
>>> names_of_parameters('sqrt_scale')
[['epsilon'], []]
Tabulated scaling function¶
1-body bond order factor of the type
where \(s_i(\Sigma)\) is a tabulated function. The tabulation works similarly to the Tabulated potential.
Keywords:
>>> names_of_parameters('table_scale')
[[id, range, scale], []]
Coordination bond order factor¶
2-body bond order factor defined as
The coordination of an atom is simply the sum of the proximity functions. This is a parameterless (besides cutoffs) 2-body bond order factor.
Keywords:
>>> names_of_parameters('neighbors')
[[], []]
Power decay bond order factor¶
2-body bond order factor defined as
This is a density-like bond factor, where the contributions of atomic pairs decay with interatomic distance according to a power law. In form, it is similar to the Power decay potential potential.
Keywords:
>>> names_of_parameters('power_bond')
[[], [a, n]]
Tabulated bond order factor¶
2-body bond order factor of the type
where \(t(r)\) is a tabulated function. The tabulation works similarly to the Tabulated potential.
Similarly, to tabulate bond scaling, use the Tabulated scaling function.
Keywords:
>>> names_of_parameters('table_bond')
[[], [id, range, scale]]
Tersoff bond order factor¶
Pairwise 3-body bond order factor defined as
where r and theta are distances and angles between the atoms. This rather complicated bond factor takes also into account the directionality of bonds in its angle dependency.
Keywords:
>>> names_of_parameters('tersoff')
[['beta', 'eta'], ['a', 'c', 'd', 'h', 'mu']]
List of methods¶
Below is a list of methods in BondOrderParameters, grouped according to the type of functionality.
Parameter handling¶
- accepts_parameters()
- get_bond_order_type()
- get_cutoff()
- get_cutoff_margin()
- get_number_of_parameters()
- get_parameter_names()
- get_parameter_value()
- get_parameter_values()
- get_parameters_as_list()
- get_soft_cutoff()
- set_cutoff()
- set_cutoff_margin()
- set_parameter_value()
- set_parameter_values()
- set_parameters()
- set_soft_cutoff()
Full documentation of the BondOrderParameters class¶
- class pysic.interactions.bondorder.BondOrderParameters(bond_order_type, cutoff=0.0, cutoff_margin=0.0, parameters=None, symbols=None)[source]¶
Class for representing a collection of parameters for bond order calculations.
Calculating bond order factors using Tersoff-like methods defined in Coordinator requires several parameters per element and element pair. To facilitate the handling of all these parameters, they are wrapped in a BondOrderParameters object.
The object can be created empty and filled later with the parameters. Alternatively, a list of parameters can be given upon initialization in which case it is passed to the set_parameters() method.
Parameters:
- bond_order_type: string
- a keyword specifying the type of the bond order factor
- soft_cut: double
- The soft cutoff for calculating partial coordination. Any atom closer than this is considered a full neighbor.
- hard_cut: double
- The hard cutoff for calculating partial coordination. Any atom closer than this is considered (at least) a partial neighbor and will give a fractional contribution to the total coordination. Any atom farther than this will not contribute to the neighbor count.
- parameters: list of doubles
- a list of parameters to be contained in the parameter object
- symbols: list of strings
- a list of elements on which the factor is applied
- accepts_parameters(params)[source]¶
Test if the given parameters array has the correct dimensions.
A bond order parameter can contain separate parameters for single, pair etc. elements and each class can have a different number of parameters. This method checks if the given list has the correct dimensions.
Parameters:
- params: list of doubles
- list of parameters
- accepts_target_list(targets)[source]¶
Tests whether a list is suitable as a list of targets, i.e., element symbols and returns True or False accordingly.
A list of targets should be of the format:
targets = [[a, b], [c, d]]
where the length of the sublists must equal the number of targets.
It is not tested that the values contained in the list are valid.
Parameters:
- targets: list of strings or integers
- a list whose format is checked
- add_symbols(symbols)[source]¶
Adds the given symbols to the list of symbols.
Parameters:
- symbols: list of strings
- list of additional symbols on which the bond order factor acts
- get_level()¶
Returns the level of the factor, i.e., is it a per-atom or par-pair factor.
- get_number_of_parameters()[source]¶
Returns the number of parameters the bond order parameter object contains.
- get_number_of_targets()[source]¶
Returns the (maximum) number of targets the bond order factor affects.
- get_parameter_value(param_name)[source]¶
Returns the value of the given parameter.
Parameters:
- param_name: string
- name of the parameter
- get_parameter_values()[source]¶
Returns a list containing the current parameter values of the potential.
- get_parameters_as_list()[source]¶
Returns the parameters of the bond order factor as a single list.
The generated list first contains the single element parameters, then pair parameters, etc.
- includes_scaling()¶
Returns True iff there are scaling paramters.
- set_cutoff(cutoff)[source]¶
Sets the cutoff to a given value.
This method affects the hard cutoff.
Parameters:
- cutoff: double
- new cutoff for the bond order factor
- set_cutoff_margin(margin)[source]¶
Sets the margin for smooth cutoff to a given value.
This method defines the decay interval \(r_\mathrm{hard}-r_\mathrm{soft}\). Note that if the soft cutoff value is made smaller than 0 or larger than the hard cutoff value an InvalidParametersError is raised.
Parameters:
- margin: double
- The new cutoff margin
- set_parameter_value(parameter_name, value)[source]¶
Sets a given parameter to the desired value.
Parameters:
- parameter_name: string
- name of the parameter
- value: double
- the new value of the parameter
- set_parameter_values(values)[source]¶
Sets the numeric values of all parameters.
Parameters:
- params: list of doubles
- list of values to be assigned to parameters
- set_parameters(params)[source]¶
Sets the numeric values of all parameters.
Equivalent to set_parameter_values().
Parameters:
- params: list of doubles
- list of values to be assigned to parameters
- set_soft_cutoff(cutoff)[source]¶
Sets the soft cutoff to a given value.
Note that actually the cutoff margin is recorded, so changing the hard cutoff (see set_cutoff()) will also affect the soft cutoff.
Parameters:
- cutoff: double
- The new soft cutoff